Below you'll find a list of all posts that have been tagged as “1st prize”
Play the movie while looking at the small white speck in the center of the ring. At first, the ring is motionless and it’s easy to tell that the dots are changing color. When the ring begins to rotate, the dots suddenly appear to stop changing. But in reality they are changing the entire time. Take a look.
In this video, wooden balls roll up the slopes just as if they are pulled by a magnet. The behavior of the balls seems impossible, because it is against the gravity. The video is not a computer graphic, but a real scene. What is actually happening is that the orientations of the slopes are perceived oppositely, and hence the descending motion is misinterpreted as ascending motion. This illusion is remarkable in that it is generated by a three-dimensional solid object and physical motion, instead of a two-dimensional picture.
In baseball, a curveball creates a physical effect and a perceptual puzzle. The physical effect (the curve) arises because the ball’s rotation leads to a deflection in the ball’s path. The perceptual puzzle arises because the deflection is actually gradual but is often perceived as an abrupt change in direction (the break). Our illusions suggest that the perceived “break” may be caused by the transition from the central visual system to the peripheral visual system. Like a curveball, the spinning disks in the illusions appear to abruptly change direction when an observer switches from foveal to peripheral viewing.
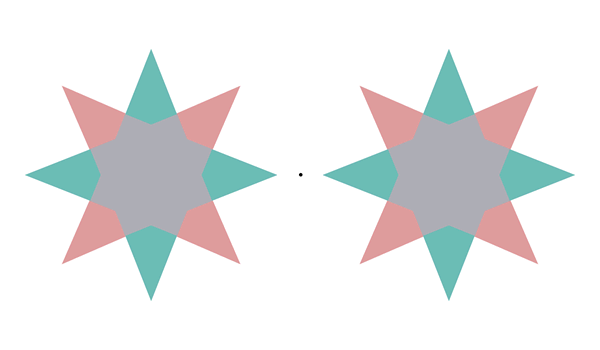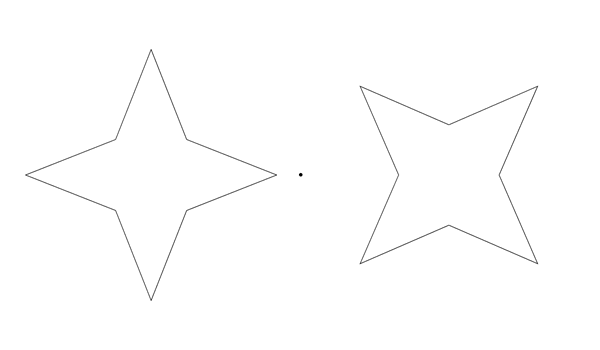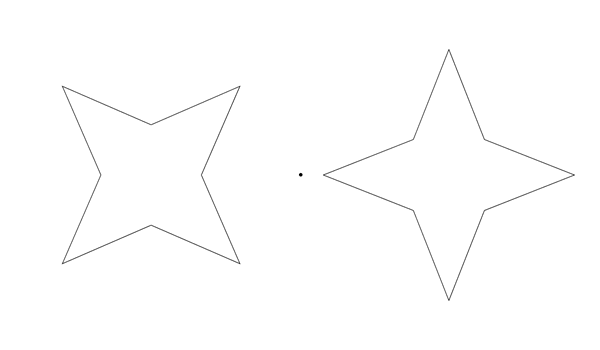
To do:
Fixate your gaze on the center of one of the figures and stare at it for some time (20-30 seconds) while it cycles (without moving your eyes). After several iterations you’ll start noticing that the empty outlines fill in with ghostly redish or bluish colors! These illusory colors are called “afterimages”. Interestingly, the colors of the afterimages vary, which is puzzling because they come from the same original figure. Moreover, the shape of the outlines determines the filled-in color, which is complementary to the color of the same shape in the original figure.
What’s happening?
It is well known that viewing a colored surface can induce a vivid afterimage of the complementary color (for example, the color red induces a greenish/bluish afterimage). Our illusion shows that a colored image can produce different colored afterimages at the same retinal location. The perceived afterimage colors depend on the contours that are presented after the colored image. More specifically, the illusion shows that the afterimage colors spread and mix between those contours. In addition, alternating different contours after the original colored image causes rapidly switching afterimage colors.
Read more about the illusion and possible explanations.
Van Lier, Vergeer, Anstis, 2009, Filling-in afterimage colors between the lines, Current Biology, 19 (8), R323-R324.
Here is a novel illusion that is as striking as it is simple. The two images of the Leaning Tower of Pisa are identical, yet one has the impression that the tower on the right leans more, as if photographed from a different angle. The reason for this is because the visual system treats the two images as if part of a singlescene. Normally, if two adjacent towers rise at the same angle, their image outlines converge as they recede from view due to perspective, and this is taken into account by the visual system. So when confronted with two towers whose corresponding outlines are parallel, the visual system assumes they must be diverging as they rise from view, and this is what we see. The illusion is not restricted to towers photographed from below, but works well with other scenes, such as railway tracks receding into the distance. What this illusion reveals is less to do with perspective, but how the visual system tends to treat two side-by-side images as if part of the same scene. However hard we try to think of the two photographs of the Leaning Tower as separate, albeit identical images of the same object, our visual system regards them as the ‘Twin Towers of Pisa’, whose perspective can only be interpreted in terms of one tower leaning more than the other.
Leaning tower illusion Frederick A. A. Kingdom, Ali Yoonessi, Elena Gheorghiu Scholarpedia 2007. 2(12):5392.
The Leaning Tower illusion: a new illusion of perspective Frederick A. A. Kingdom, Ali Yoonessi, Elena Gheorghiu Perception. 2007. 36(3):475-477
An object (e.g. airplane) is turning on a surround (greenhouse), which is swaying back and forth. Observe the rotation of the object. Is it turning smoothly all the time? Or does it “freeze” from time to time? Convince yourself by covering the swaying surround that the object is really turning continuously. If the object is swaying back and forth and the surround is turning continuously we do not perceive a slow-down of the surround. Assuming a stable surround, our visual system probably uses the surround as a reference to measure motion of the included objects.
Read more about the illusion and possible explanations
See an interactive version of the The Freezing Rotation Illusion at Michael Bach’s “Optical Illusions & Visual Phenomena” website
The Freezing Rotation IllusionMax R. DürstelerNature Precedings 2007. 371.1
A number of well-known motion illusions arise when luminance modulates next to a stationary edge (e.g., Anstis and Rogers, 1975; Gregory and Heard, 1983). Here, we reduce these phenomena to four novel elemental conditions and show how these conditions can be combined (like building blocks) to generate an infinite number of new illusory configurations.
Click on the “Elemental Conditions” button in the accompanying movie . In the top two panels, the luminance of the edge modulates next to stationary black or white center fields; in the bottom two panels , the luminance of the center modulates next to black or white stationary edges (Figure 1A shows one frame of the movie). In all four conditions, the fields appear to move even though they maintain a fixed spatial position. The apparent direction of motion may seem counter-intuitive: when the luminance of a modulating edge is similar to the luminance of the center, the motion is outward, whereas when the luminance of a modulating center is similar to the luminance of the edge, the motion is inward.
Read more about the illusion and possible explanations
Visual illusions based on single-field contrast asynchronies Arthur G. Shapiro, Justin P. Charles & Mallory Shear-Heyman Journal of Vision. 2005. 5:764-82
